Largest Container
You are given an array of numbers, each representing the height of a vertical line on a graph. A container can be formed with any pair of these lines, along with the x-axis of the graph. Return the amount of water which the largest container can hold.
Example:
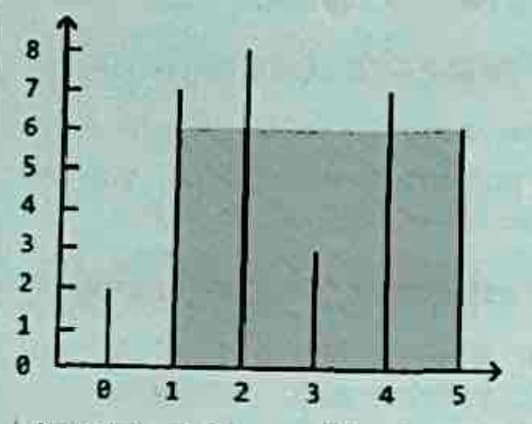
Input: heights = [2, 7, 8, 3, 7, 6]
Output: 24
Intuition
If we have two vertical lines, heights[i] and heights[j],the amount of water that can be contained between these two lines is min(heights[i], heights[j]) * (j - i), where j - i represents the width of the container. We take the minimum height because filling water above this height would result in overflow.
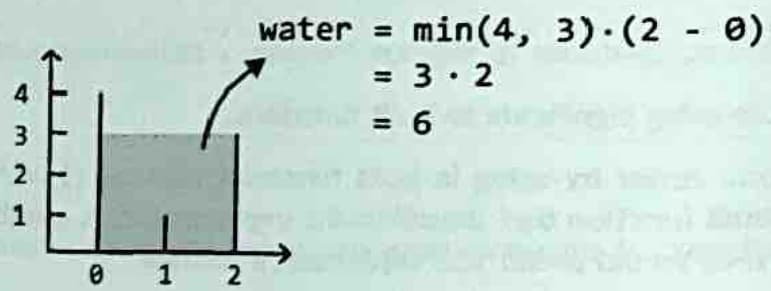
In other words, the area of the container depends on two things:
- The width of the rectangle.
- The height of the rectangle, as dictated by the shorter of the two lines.
The brute force approach to this problem involves checking all pairs of lines, and returning the largest area found between each pair:
Searching through all possible pairs of values takes time, where n denotes the length of the array. Let's look for a more efficient solution.
We would like both the height and width to be as large as possible to have the largest container.
It'snot immediately obvious how to find the container with the largest height,as the heights of the lines in the array don't follow a clear pattern. However, we do know the container with the maximum width: the one starting at index O and ending at index n -1.
So, we could start by maximizing the width by setting a pointer at each end of the array. Then, we can gradually reduce the width by moving these two pointers inward, hoping to find a container with a larger height that potentially yields a larger area.This suggests we can use the two-pointer pattern to solve the problem.
Moving a pointer inward means shifting either the left pointer to the right,or the right pointer to the left, effectively narrowing the gap between them.
Consider the following example:
The widest container can store an area of water equal to 10. Since this is the largest container we've found so far,let's set max_water to 10.
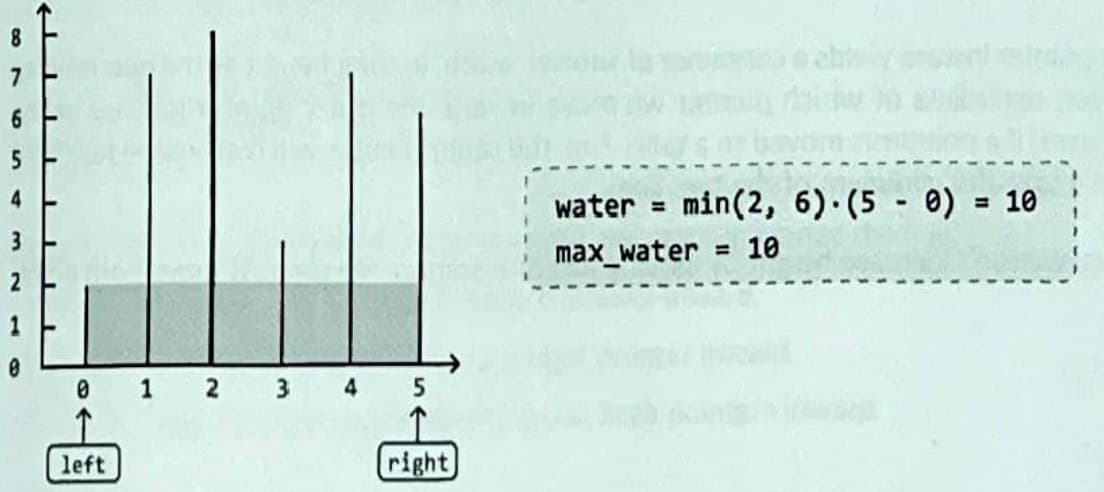
How should we proceed? Moving either pointer inward yields a container with a shorter width.
This leaves height as the determining factor. In this case, the left line is shorter than the right line, which means that the left line limits the water's height.Therefore, to find a larger container, let's move the left pointer inward:
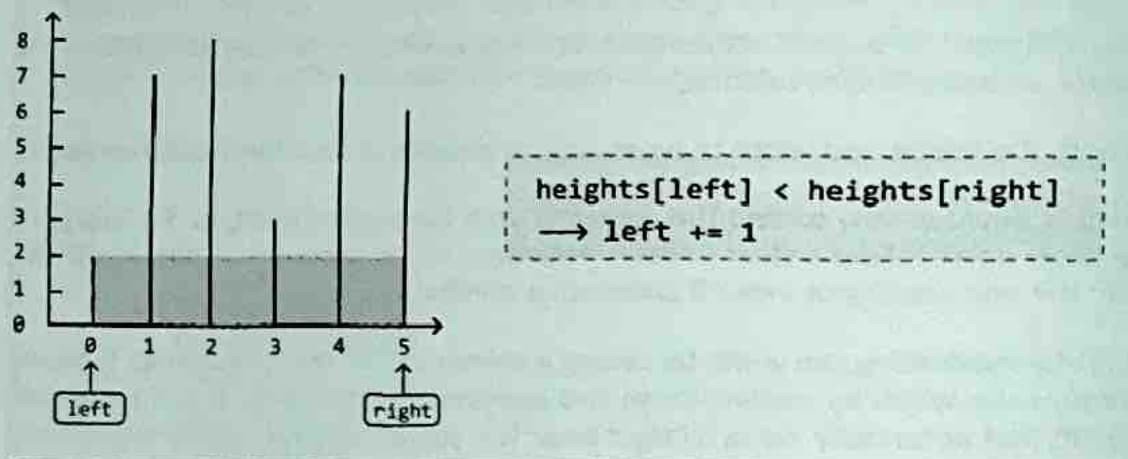
The current container can hold 24 units of water,the largest amount sofar.So,et's update max_water to 24. Here, the right line is shorter,limiting the water's height. To fnd a larger container,move the right pointer inward:
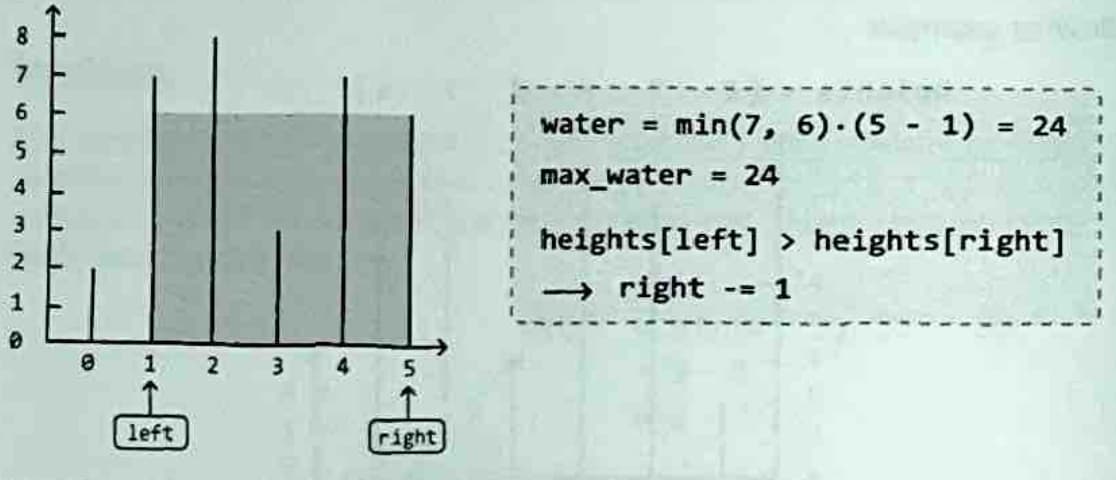
After this,we encounter a situation where the height of the left and right lines are equal. In this situation, which pointer should we move inward? Well, regardless of which one, the next container is guaranteed to store less water than the current one. Let's try to understand why.
Moving either pointer inward yields a container of shorter width, leaving height as the determining factor. However, regardless of which pointer we move inward, the other pointer remains at the same line. So, even if a pointer is moved to a taller line, the other pointer will restrict the height of the water, as we take the minimum of the two lines.
Therefore since we can't increase height by moving just one pointer, we can just move both pointers inward:
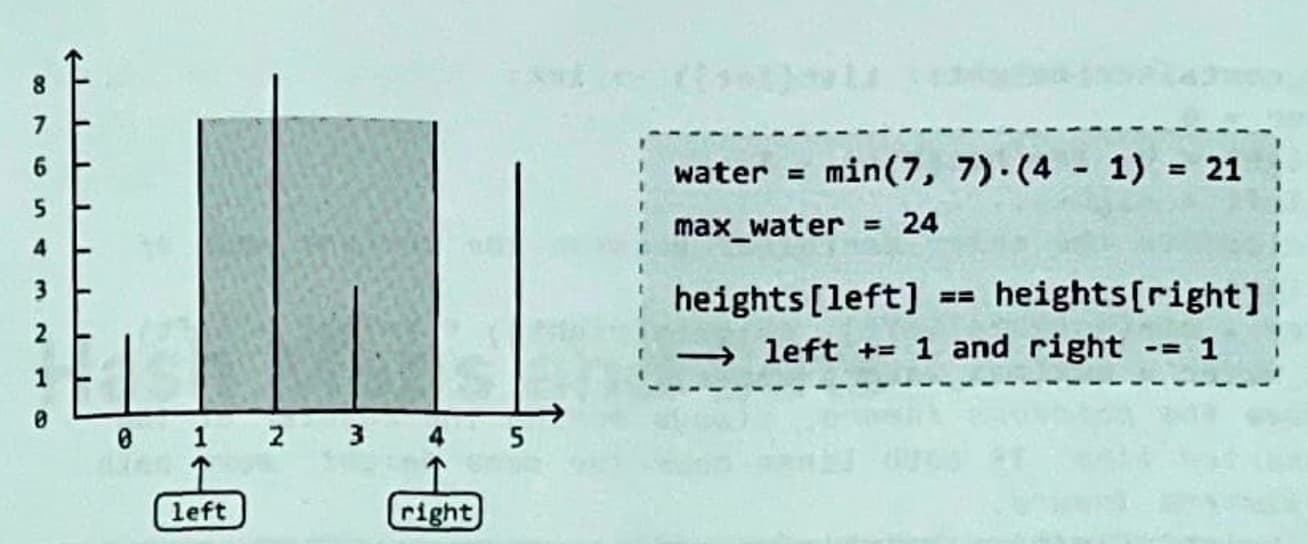
Now, the right line is limiting the height of the water. So, we move the right pointer inward:

Finally, the left and right pointers meet.We can conclude our search here and return max_water:
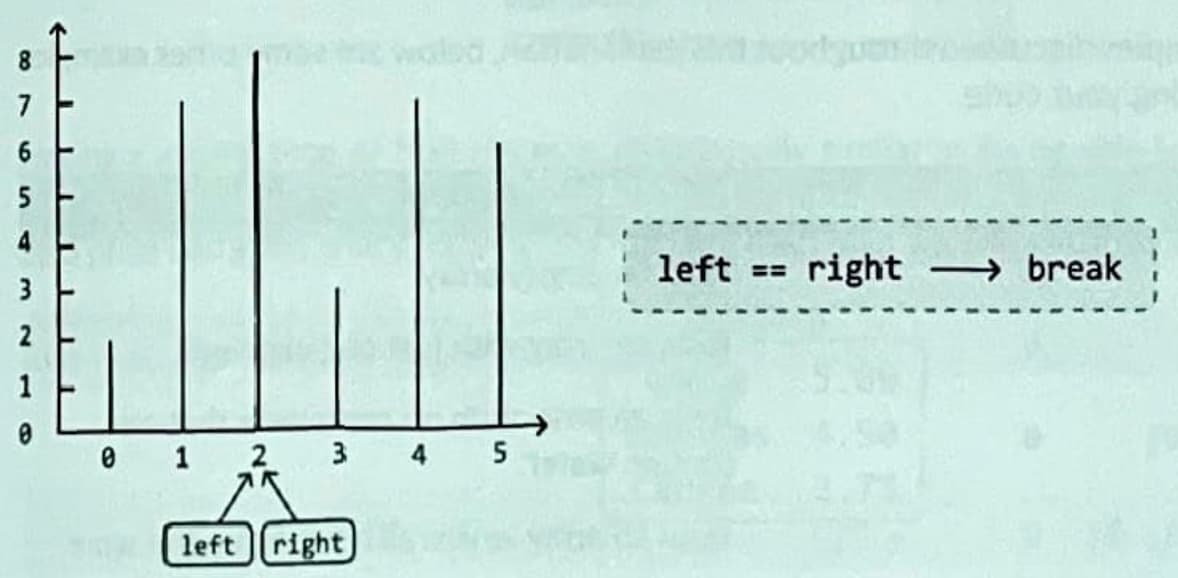
Based on the decisions taken in the example, we can summarize the logic:
- If the left line is smaller, move the left pointer inward.
- If the right line is smaller, move the right pointer inward.
- If both lines have the same height, move both pointers inward.
Implementation
Complexity Analysis
Time complexity: The time complexity of largest_container is because we perform approximately n iterations using the two-pointer technique.
Space complexity: We only allocated a constant number of variables, so the space complexity is
Test Cases
In addition to the examples discussed throughout this explanation, below are some other examples to consider when testing your code.
| Input | Expected output | Description |
|---|---|---|
| heights = [] | 0 | Tests an empty array. |
| heights = [1] | 0 | Tests an array with just one element. |
| heights = [0, 1, 0] | 0 | Tests an array with no containers that can contain water. |
| heights = [3, 3, 3, 3] | 9 | Tests an array where all heights are the same. |
| heights = [1, 2, 3] | 2 | Tests an array with strictly increasing heights. |
| heights = [3, 2, 1] | 2 | Tests an array with strictly decreasing heights. |